Ian Gibbins
FirstEDA

Ian Gibbins
FirstEDA
Assertion-based verification (ABV) is a technique which can dramatically reduce the verification process compared with traditional methods
—
It has been predominantly employed in the ASIC world but due to the ever increasing complexity of FPGA devices, is proving vital in the FPGA verification flow.
However, before we begin to celebrate the possibility of a dramatic reduction in the project verification cycle, we need to understand assertions and how they can be integrated effectively into a verification methodology.
In the interests of technical digestion, this introduction to assertions will be split into two parts. The first part will explain what an assertion is, talk about the languages and develop the basic terms and ideas. In part two we dig deeper and introduce the use of implication and the notion of ‘vacuous truths’ along with asserts and covers.
The simplest definition of an assertion is ‘An abstract representation of device behaviour which is useful in specification, verification and implementation…’
Later on we will see that this definition can be expanded into a more accurate description but this one will do for now.
There are two languages available with practical applications of expressing assertions, namely Property Specification Language (PSL) and SystemVerilog Assertion subset (SVA).
PSL is available for VHDL, Verilog, SystemVerilog and SystemC and is a subset of VHDL-2008.
SVA is an assertion related subset of the SystemVerilog language and is based upon the Superlog and OpenVera donations. Its assertions and properties features also borrow from PSL.
Both languages are IEEE standards.
VHDL designers can use both SVA and PSL but normally opt for PSL as it can be placed directly into the VHDL code and aid the documentation of the design whereas SVA cannot. Also, PSL is now part of the VHDL standard (2008) and so it means that only one language needs to be used.
Verilog designers can use both PSL and SVA but normally use SVA as it has more functionality available when placed directly into the Verilog code than PSL. Also, SystemVerilog and Verilog are now merged into one single standard – SystemVerilog.
The good news is that PSL and SVA properties look pretty much the same.
Assertions are already an established and popular method of verification in ASIC design and therefore, FPGA designs can learn from this arena. Importantly, they are governed by IEEE standards (PSL, SystemVerilog and VHDL).
Assertions are relatively simple to learn and implement and much easier than having to deal with class, objects, inheritance etc. as in object oriented programming. They are based upon the design specification which will be familiar to you as a designer and so easier to implement.
Assertions create an additional layer of safety in simulation as they are a reference to the original specification and can be very useful when making synthesis and implementation iterations.
Assertions essentially create ‘live documentation’ in how they are written which makes the management of the design easier. They are very easy to read and interpret which makes sharing with design teams much more manageable.
All tools allow you to place assertions in separate units or files and ‘bind’ them to your regular RTL code. Verification engineers like this idea, as it allows file independence, whereas HDL designers generally prefer to place the assertions directly into the code to reduce the amount of files required.
Most simulators allow you to place assertions directly in the RTL code. For PSL this is represented as comments. For SystemVerilog, assertions can be placed directly into the code.
For example: –psl property p1 is… or //psl property p2 is…
VHDL-2008 allows PSL assertions to be placed directly into the code (without the need for comments).
Care needs to be taken when placing the assertions into the code as synthesis tools generally do not support certain assertions and so the use of synthesis pragmas are required to manage them.
The term ‘Assertion-Based Verification’ (ABV) is generally used to describe the whole verification process, but it deals with more than just assertions.
The flow is made up of sequences, properties, assertions and covers.
The basic idea of ABV is the ‘property’. A property is the formalised description of a certain behaviour of your design, for example ‘a broken window triggers alarm’ or ‘security responds to alarm in 30 seconds’.
Properties can be used by verification tools in many ways, by ‘asserting’ a property verifies that bad things do not happen e.g. ‘assert [that] broken window always triggers alarm’.
Alternatively, using a ‘cover’ verifies that good things happen e.g. ‘cover [the] response to triggered alarm in 30 seconds’.
Digging deeper into the properties, if you look at a typical digital design specification, it is already full of design properties expressed in plain English. As a designer, you rewrite these properties into HDL with the correct hardware implementation in mind.
So properties, assertions and covers represent the pure behaviour of the design (desired or undesired). As we have said, they can act as very efficient documentation of the design, as well as being a reference during design verification. They are also accepted by a variety of functional and formal verification tools.
We now need to look at how a property is defined and how it uses the principles of ‘temporal logic’.
Temporal logic can be thought of as boolean logic with an added time dimension.
If we use ‘discrete time’, then properties represent ‘sequences of states’ of the design. Please note that all popular property-based design (PBD) /ABV solutions operate on sampled values of objects in the design.
In order to express this relationship in time, properties use ‘temporal’ or ‘modal’ operators e.g. next, finally, globally, until etc.
Next we need to understand how properties can be built up.
Boolean type expressions, which we are all familiar with, are part of the make up of properties, but rather the simplest part. We also need to understand ‘sequences’.
A ‘sequence’ is generally recognised as the basic temporal building block of properties representing a succession of design states at discrete time points.
A typical sequence represents a simple execution path in the design.
To create realistic properties from simple sequences you can:
Once the design property is formalised, all tools can use those properties in one of two directives:
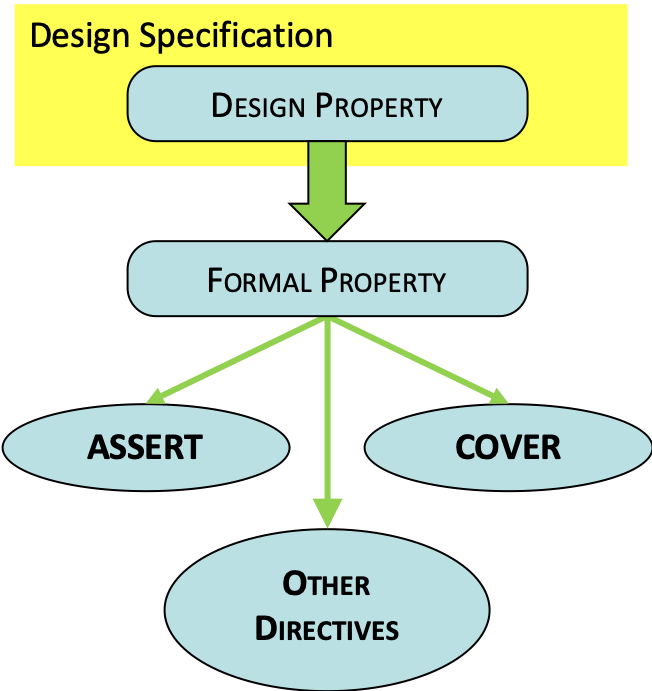
Assert – which raises an alarm when the property does not hold.
Cover – which confirms that the property was successfully tested.
Some tools (mainly formal verification but also some simulators) allow more directives e.g. to control design stimulus or restrict environmental conditions (assume, restrict, fairness etc).
Now we have looked at the basic elements of properties and sequences, let us look at how to build practical assertions.
As we have mentioned, the very basic properties are ‘sequences’ with strict linear time flow.
The linear time flow is required for simulation and therefore the jumping back and forth in time for properties is not possible, as it would make simulation impossible.
Each node of the sequence represents a state of your design:
In order to complete the sequence, you have to specify how to tie those nodes together. So, let us look at some ‘sequence’ property facts.
The simplest sequence is a boolean expression, but more frequently you will glue together several expressions to form a complex sequence that ‘spreads in time’.
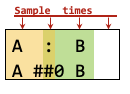
To make elements stick together at the same clock, use ‘fusion’ (:) in PSL or ‘zero clock delay’ (##0) in SVA.
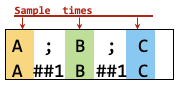
To introduce one cycle break between elements, use ‘concatenation’ (;) in PSL or ‘one cycle delay’ (##1) in SVA.
You can specify longer delays using a range of values (##[m:n]) in SVA.
PSL uses the ‘consecutive repetition operator’ (<sequence>[*m to n]) to specify a ‘range of values’ delay. If there is no sequence to repeat then it is assumed that ‘True’ is the argument of repetition.
Now we have mentioned repetition, let us look at this more formally.
If the same condition should hold for more than one cycle, then we can use the ‘consecutive repetition operator’ instead of repeating the condition using concatenation or one cycle delay.
The operator looks identical in PSL and SVA: Sequence [* Number_or_Range].
A simple form with a number says that the sequence should be repeated (hold) a given number of times: A[*7].
A range version says that the sequence should hold for any number of cycles within the natural range (to specify infinite upper bound, use ‘inf’ in PSL or ‘$’ in SVA): B[*1 to inf] B[*1:$]
Let us illustrate with an example:

Here we see an example of repetition in action, along with the equivalent sequence without repetition and showing the same sequence for PSL and SVA.
All property languages use discrete time, which means that a clocking or sampling method must be specified.
If no clocking is specified, then the fastest available tool default is applied, which in the case of a simulator may be the clock with a period that is equal to the simulation resolution.
If one clocking method is used in the majority of properties, then you can specify ‘default clock’.
To specify a clocking event, use the ‘@<clock condition> at the end of a sequence in PSL or at the beginning in SVA.
For the clock condition, use the clock detector preferred in the native HDL, e.g. ‘rising_edge’ function in VHDL or ‘negedge’ in Verilog.
We also need to be able to handle resets, as sometimes you could be in the middle of a property evaluation and a reset occurs which would cause an assertion failure or other unwanted situation.
Fortunately, both PSL and SVA provide a mechanism for abandoning property evaluation without adverse effects.
PSL allows the addition of ‘async_abort’ or ‘sync_abort’ operator and reset condition at the end of a property.
always (({(A);(B)}) async_abort C=’1′) @rising_edge(CLK);
SVA allows the addition of ‘disable iff (condition)’ phrase at the beginning of the property.
@(posedge CLK) disable iff (C) A ##1 B;
So to summarise on clocks and resets:
There are no default resets in properties, but you can have default clocks (sampling events).
The textual order of applying resets and clocks to properties in SVA is a mirror image of the order in PSL.

We have introduced assertions and seen that both the PSL and SVA properties are similar and resemble the design requirements.
We have developed the basic terms and ideas of assertions and discussed sequences, properties, assertions and covers and how they form design properties. We also learned how a property is defined and how it follows the principles of temporal logic. Finally, we began to build some practical assertions to understand what we have introduced and discussed.
If you have enjoyed this introduction, you can look forward to part two which will develop the use of implication in assertions and its importance in assertions and use in simulation.